Blindzeit

Often times, the words we use every day get taken for granted. When a toddler learns about a new object in the world, they might see it, touch it, hear it or taste it. They store those feelings somewhere in the memory. At some point, a parent may point their finger at that object and say the name that is commonly used in verbal language (i.e. “dog”). The child will then have an abstraction of that object that allows them to converse with other humans who know the same language, however, at the end of the day the word “dog” is just a pointer to the conscious experience stored in the back of the toddler’s mind.

Numbers are different than the words we use because they are abstract concepts. Numbers are fundamental laws of our universe that we discover and label. When we see the number 5, we might imagine 5 banana or something along those lines but we can also associate it with intangible things like 5 seconds.

This blog post will attempt to demonstrate to you that this many of bananas

can be represented as

11

When humans first began counting, we used our fingers to facilitate. That’s why it makes sense that most civilizations throughout history have based their number systems around the number 10. If our species had evolved to have eight fingers like Mickey Mouse, we would have most likely created our number system differently. Here is a demonstration of how our number system neatly fits around the number 10.

10^1 = 10

10^2 = 100

10^3 = 1,000

10^4 = 10,000

10^5 = 100,000

Inventing Numbers

It’s believed that numbers were first used as a ledger to keep track of ownership of different items. For example, if someone owned 6 cows it might be represented as 6 drawings of cows.

That would be a lot of work to draw 6 cows. At some point it might make sense to symbolize the number of cows as scratch marks like this:

||||||

This works much better, but if there were 30 cows it again starts to become tedious.

||||||||||||||||||||||||||||||||||||||||||

Once you come to realization that these scratch marks are driving you insane, you might attempt to come up with a better approach. At that moment, you have invented a number system.

The Roman numeral system is still used today. In the Roman numeric system 36 cows would be represented like this:

XXXVII

In the Roman System

X = 10

V = 5

I = 1

When we think about the number system used today (base ten, or decimal), and I mean really think about it, you will realize that we do not have a special number for the number ten. What we do have that is a special number is 0. The number zero is one of the most important inventions of all time. The number 0 allows us to differentiate between 35, 305, and 350.

When we look at the number 8,425 we can write the components of it like this:

8000 +

400 +

20 +

5 =

8,425

We can also represent it like this:

8 x 1000 +

4 x 100 +

2 x 10 +

5 =

8,425

Or even further:

8 x 10^3 +

4 x 10^2 +

2 x 10^1 +

5 x 10^0 =

8,425

We can see how the base ten system really is nice. As stated before, humans developed their number system based on the number of fingers they have (10). This is a base 10 system:

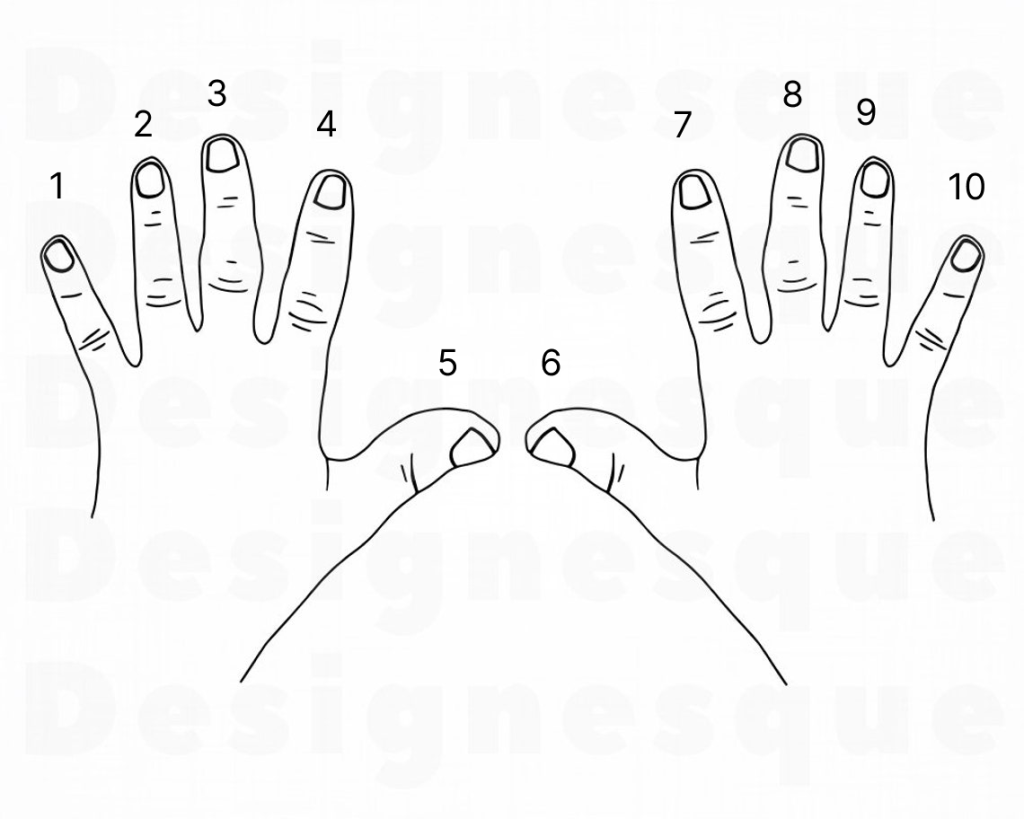
It is so embedded in us that when we think of 10 bananas, we cant help but think of this many bananas

In a universe of Mickey Mouses who have 8 fingers, they would likely use a base 8 system (or an octal system). In a base 8 system, there would be no need for this symbol.

9

Additionally there would be no need for a symbol like this:

8

In our decimal system, there is no special symbol for ten, and for an octal system there is no special symbol needed for the number eight.

Our decimal system is counted like follows: 0,1,2,3,4,5,6,7,8,9 and then 10. In an octal system it would be 0,1,2,3,4,5,6,7 and then…10! In an octal system the number after 7 is 10. The difference is that in an octal system, the number 10 doesn’t mean the number of fingers a human has but rather the number of fingers Mickey Mouse has:

It can be helpful to avoid confusion by pronouncing numbers like 10 as one zero and 15 as one five.

Here are some ways things would be represented in an octal system.

A bakers dozen is 15.

The “sweet” birthday celebration is 20.

the hours in a day is 30.

Now lets take things a step further and imagine that penguins were to create their own number system. There would be no need for the number two! In fact, the next number after 1 would be…10 again! This is a binary system.

In a binary system, we count like this:

0,1,10,11,100,101,110,111,1000,1001,1010,1011…

The numbers look large but they aren’t, they are rather long.

In binary:

The number of heads a human has is 1.

The number of eyes that a human has is 10.

The number of sides on a triangle is 11.

The number of sides on a square is 100.

By understanding the root of our own base ten number system, it allows us to understand the other universes with other numbering systems. Each of these other number systems are completely valid and it happens to be the case that in the world of modern computers, machines use a binary system.